Picture this:
You’re coding a game that requires tracking across an X,Y grid, say Tetris or Connect 4. You’ve almost got your code complete when you run into a brick wall that you didn’t prepare for: How to win.
When accounting for combinations on a coordinate grid, the most tedious way to go about it is to account for EVERY SINGLE COMBINATION. Not to mention, if the grid is too big, you wouldn’t even have enough memory for it. What do you do?
Doing The Math
I’m in the process of making a Connect 4 remake,so 4 disks of the same color have to be next to each-other in order for one player to win.
I might make a ‘stacking’ tutorial one day.
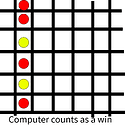
Now, you might be thinking: Why can’t you just make it so that once 4 are placed, the player wins? You could, but then it would create a bug like this:
The disks have to be next to each-other to actually be a win. This complicates things.
In a 7x7 Grid, there are 4 winning combinations for both vertical and horizontal placement.
Yes, I know that typically Letters represent rows and numbers are columns, but that’s not the way I did it.
For a column, it could be
A1 | A2 | A3 | A4
A2 | A3 | A4 | A5
A3 | A4 | A5 | A6
A4 | A5 | A6 | A7
And for each row, it could be
A1 B1 C1 D1
B1 C1 D1 E1
C1 D1 E1 F1
or
D1 E1 F1 G1
So 4 combinations of 4 per column.
To assign values to these combinations, we’ll use the SUM of the 4 numbers! This will assign unique values to each combination and also allowing them to be concated, or simplified using repetiton with slight changes, in block code!
1+2+3+4 = 10
2+3+4+5 = 14
3+4+5+6 = 18
4+5+6+7 = 22
So now that we have the sum values for each combination, we’re done, right? Wrong! There’s still another step to do, and that’s accounting for the possibility of the presences of other disks. Since a red disk could be in-between 2 yellow ones, that means we’d have to also include the sum of the basic combination + any disk that’s at least 2 away.
So, we’d also have to add
1+22
=23
2+22=24
and
1+2+22 = 25
for 4567.
Likewise, we’d add
1+18 =19 for 3456,
7+14 = 21 for 2345,
and
6+10 = 16,
7+10 = 17,
and 6+7+10 = 23 for 1234.
So now, we HAVE to be done, right??
With the math, yes.
The Code
Once you’ve gotten through the process of proofing and checking your math to make sure there’s no unregistered solutions, it’s pretty smooth sailing if you’ve got a basic grip on GKC’s block code system, and concatenation.
The devices you’ll need for 1 row/column are
- 2 triggers
- 2 property devices
Simple, and memory-efficient – 1 set only takes up 1100 memory!
Name your 2 property devices something like A and A2 or 1A and 1B depending on if they’re horizontal or vertical.
In my connect 4 game, I have a trigger connected to a button. The trigger broadcasts on a few channels, one of which signals the 2 triggers that we’re using in this set.
The reason I’m saying this is because you’ll need something to broadcast on a channel/wired to your trigger. Have both of them set
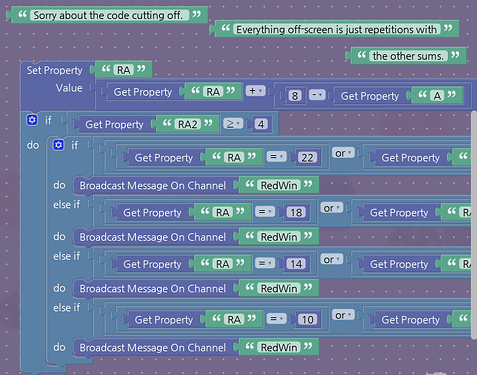
Go into the ‘Blocks’ menu in one of your triggers, and input code that looks something like so:
This will make it so that ‘RA2’ Increases once it receives the broadcast.
Now, go into your other trigger. The code on this one is a lot more complex.
The reason we need the RA > 4 is because it prevents a lot of bugs with the sums. CHANGE THE RA2 VALUE TO HOWEVER MANY VALUES ARE IN ONE SOLUTION IF NEEDED!! THE 8 REPRESENTS THE NUMBER OF COLUMNS/ROWS + 1.
In the ‘do’ sections of your blocks, have it broadcast on the channel that corresponds to each solution. Now copy the triggers, make more property managers, and change the block code accordingly until each row and column is accounted for! After you have all this set up, your solutions should be fully tracked!
This is my MOST COMPLICATED GUIDE.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10